What Is The Value Of X 50 100
kreativgebiet
Sep 23, 2025 · 5 min read
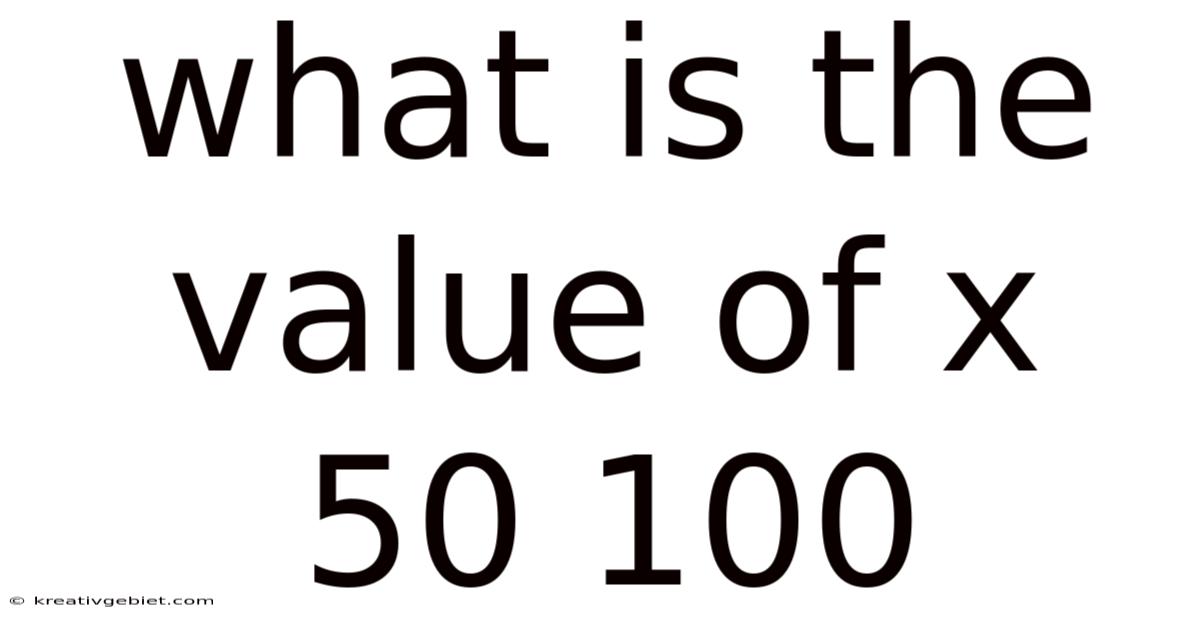
Table of Contents
Decoding the Value of x: Exploring Mathematical Relationships in Equations
This article delves into the intriguing question: "What is the value of x in the equation 50 = 100x?". Understanding how to solve for x in simple algebraic equations is fundamental to success in mathematics and numerous fields that rely on quantitative analysis. We will not only find the solution but also explore the underlying principles, providing a comprehensive understanding of the process and its applications. This will equip you with the skills to tackle similar problems and appreciate the power of algebraic manipulation.
Understanding the Equation: 50 = 100x
Before diving into the solution, let's dissect the equation itself. The equation "50 = 100x" is a simple algebraic equation, where 'x' represents an unknown variable. The equation states that 50 is equal to 100 multiplied by x. Our goal is to isolate 'x' and determine its numerical value. This involves employing basic algebraic principles, primarily focused on the concept of inverse operations.
Solving for x: A Step-by-Step Guide
Solving for 'x' requires isolating it on one side of the equation. This is achieved by performing the inverse operation on both sides of the equation, maintaining balance and ensuring the equation remains true. Here's the step-by-step process:
-
Identify the Operation: The equation shows that 'x' is being multiplied by 100.
-
Apply the Inverse Operation: The inverse operation of multiplication is division. To isolate 'x', we need to divide both sides of the equation by 100.
-
Perform the Calculation:
50 = 100x
50/100 = (100x)/100
0.5 = x
-
Solution: Therefore, the value of x is 0.5 or 1/2.
Verifying the Solution
It's always a good practice to verify your solution. Substitute the calculated value of x (0.5) back into the original equation:
50 = 100 * 0.5
50 = 50
The equation holds true, confirming that our solution, x = 0.5, is correct.
Deeper Dive: Understanding the Principles Involved
Solving this simple equation utilizes fundamental algebraic principles. Let's explore these concepts further:
-
Variables and Constants: In an algebraic equation, variables (like 'x') represent unknown quantities, while constants (like 50 and 100) are known values.
-
Inverse Operations: Every mathematical operation has an inverse. Addition and subtraction are inverse operations; multiplication and division are inverse operations. Applying inverse operations is crucial for isolating variables.
-
Maintaining Equation Balance: The golden rule of algebra is to maintain the equality of both sides of the equation. Any operation performed on one side must be performed on the other to preserve the balance and ensure the accuracy of the solution.
-
Equations as Statements of Equality: An equation is a statement that two mathematical expressions are equal. Solving the equation is about finding the value(s) of the variable(s) that make this statement true.
Expanding the Concept: More Complex Equations
While this example involved a straightforward equation, the principles applied here extend to more complex scenarios. Consider the following:
-
Equations with Multiple Variables: Equations with multiple variables require more sophisticated techniques like substitution or elimination to solve for a specific variable.
-
Equations with Exponents: Equations involving exponents require applying exponential rules and logarithmic functions to solve for the unknown variable.
-
Systems of Equations: Multiple equations with multiple variables often necessitate solving a system of equations, employing methods like substitution or elimination to find solutions that satisfy all the equations simultaneously.
-
Quadratic Equations: Equations of the form ax² + bx + c = 0 (where 'a', 'b', and 'c' are constants) require the use of the quadratic formula or factorization to find the values of x.
Real-World Applications: Where This Matters
Understanding how to solve algebraic equations is not just a theoretical exercise; it has wide-ranging practical applications across various fields:
-
Engineering and Physics: Calculating forces, velocities, and other physical quantities often requires solving complex algebraic equations.
-
Finance and Economics: Determining interest rates, investment returns, and economic models necessitates solving algebraic equations.
-
Computer Science: Programming and algorithm development often involve creating and solving algebraic equations to model real-world problems.
-
Data Analysis and Statistics: Statistical models frequently use algebraic equations to analyze data and draw meaningful conclusions.
-
Everyday Life: Many everyday situations, from calculating discounts to determining the best value in a purchase, can benefit from applying simple algebraic principles.
Frequently Asked Questions (FAQ)
Q: What if the equation was 100 = 50x?
A: The process remains the same. You would divide both sides by 50 to isolate x, resulting in x = 2.
Q: Can I multiply both sides of the equation by a number other than 1?
A: Yes, you can multiply (or divide) both sides of the equation by any non-zero number and maintain the equality. However, dividing by 100 (or 50 in the alternate example) is the most efficient way to directly isolate 'x' in this specific scenario.
Q: What if x was a negative number?
A: The method remains the same regardless of whether the solution is positive or negative. The algebraic process will yield the correct result.
Q: Are there other ways to solve this equation?
A: While division is the most straightforward approach, you could also consider it as a ratio problem. The ratio 50:100 simplifies to 1:2, leading to x = 1/2 or 0.5.
Conclusion: Mastering the Fundamentals
Solving the equation 50 = 100x, resulting in x = 0.5, may seem elementary at first glance. However, understanding the underlying principles of algebra – the use of inverse operations, maintaining equation balance, and the fundamental nature of variables and constants – is crucial for tackling more complex mathematical challenges. These foundational skills are essential for success not only in advanced mathematical studies but also in a wide array of real-world applications, demonstrating the far-reaching significance of seemingly simple algebraic operations. The ability to solve for x represents a fundamental step towards mastering algebraic manipulation and its vast potential in various fields. Continue practicing and exploring more complex equations to build your confidence and proficiency in this core area of mathematics.
Latest Posts
Latest Posts
-
A Guiding Principle Of The National Response Framework Is That
Sep 23, 2025
-
Mat 144 Module 1 Homework
Sep 23, 2025
-
4 1 Discussion Developing Visualizations For Your Story
Sep 23, 2025
-
Eocs Receive Senior Level Guidance From
Sep 23, 2025
-
Which Of The Following Undergoes Solvolysis In Methanol Most Rapidly
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 50 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.