Evaluate The Integral. 64 2 3 X X Dx 1
kreativgebiet
Sep 22, 2025 · 5 min read
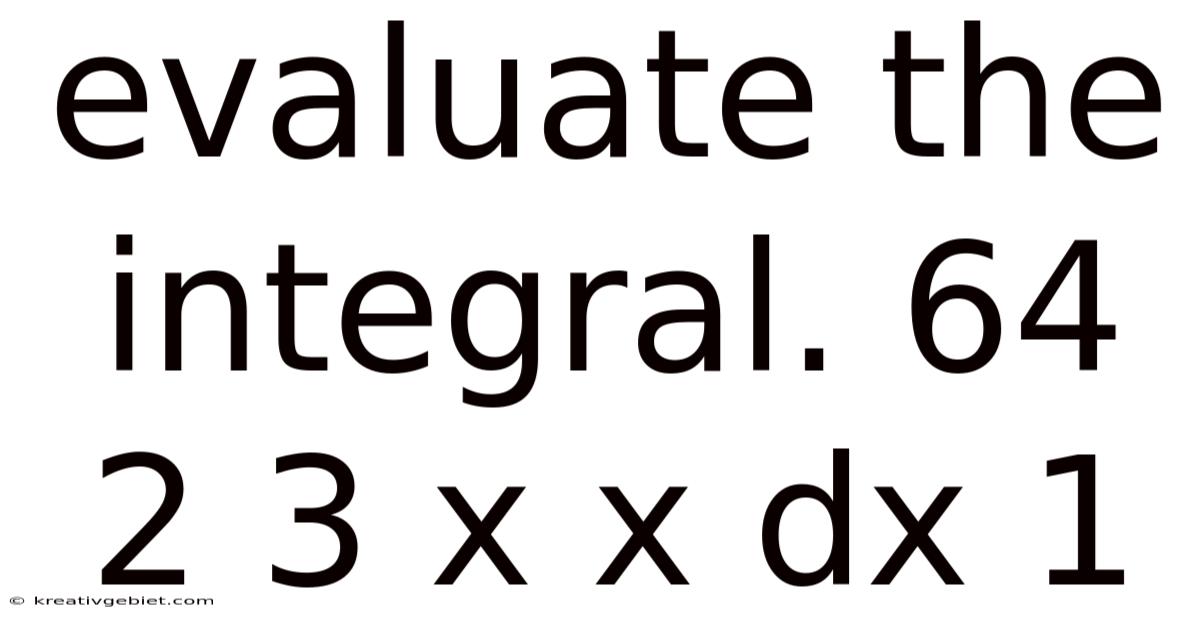
Table of Contents
Evaluating the Definite Integral: ∫₁⁶⁴ (2/3)x^(2/3) dx
This article provides a comprehensive guide on how to evaluate the definite integral ∫₁⁶⁴ (2/3)x^(2/3) dx. We will delve into the step-by-step process, explain the underlying mathematical principles, and address common questions related to integration. Understanding this process is crucial for students and professionals working with calculus and its applications in various fields like physics, engineering, and economics. The integral involves fractional exponents, which might seem daunting at first, but with a clear understanding of the power rule of integration, the solution becomes straightforward.
Introduction to Definite Integrals
A definite integral calculates the signed area between a curve and the x-axis over a specified interval. Unlike indefinite integrals which result in a general function plus a constant of integration (C), definite integrals yield a numerical value representing this area. The notation ∫ₐᵇ f(x) dx represents the definite integral of the function f(x) from x = a to x = b. 'a' and 'b' are called the lower and upper limits of integration, respectively.
In our case, we are tasked with evaluating:
∫₁⁶⁴ (2/3)x^(2/3) dx
This means we need to find the signed area under the curve y = (2/3)x^(2/3) between x = 1 and x = 64.
Step-by-Step Evaluation using the Power Rule
The fundamental theorem of calculus provides the pathway for solving definite integrals. It states that if F(x) is an antiderivative of f(x), then:
∫ₐᵇ f(x) dx = F(b) - F(a)
The key is finding the antiderivative, F(x). We'll utilize the power rule for integration, which is the inverse operation of the power rule for differentiation. The power rule states:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C (where n ≠ -1)
Let's apply this to our problem:
-
Identify the function: Our function is f(x) = (2/3)x^(2/3).
-
Apply the power rule: We add 1 to the exponent (2/3 + 1 = 5/3) and then divide by the new exponent:
∫(2/3)x^(2/3) dx = (2/3) * [x^(5/3) / (5/3)] + C = (2/3) * (3/5)x^(5/3) + C = (2/5)x^(5/3) + C
-
Find the antiderivative: The antiderivative F(x) is (2/5)x^(5/3). Note that the constant of integration (C) disappears when we evaluate a definite integral because it cancels out when subtracting F(a) from F(b).
-
Evaluate at the limits of integration: Now we apply the fundamental theorem of calculus:
F(64) - F(1) = [(2/5)(64)^(5/3)] - [(2/5)(1)^(5/3)]
-
Simplify:
(64)^(5/3) = (64^(1/3))^5 = 4⁵ = 1024
Therefore:
F(64) - F(1) = (2/5)(1024) - (2/5)(1) = (2/5)(1023) = 2046/5 = 409.2
Therefore, the value of the definite integral ∫₁⁶⁴ (2/3)x^(2/3) dx is 409.2.
Explanation with Further Mathematical Detail
The fractional exponent (2/3) represents a cube root squared. The power rule of integration extends seamlessly to fractional exponents, as demonstrated above. The process involves increasing the exponent by one and then dividing by the new exponent. This is consistent with the fundamental theorem of calculus, ensuring we find the precise area under the curve.
The constant of integration, 'C', is crucial in indefinite integration, representing the family of antiderivatives. However, in definite integration, 'C' cancels out, leaving us with a precise numerical answer.
Let's elaborate on the simplification:
- (64)^(1/3): This represents the cube root of 64, which is 4 (because 4 * 4 * 4 = 64).
- 4⁵: This is 4 raised to the power of 5, resulting in 1024.
Therefore, substituting these values back into the equation leads to the final answer of 409.2.
Practical Applications and Interpretations
Definite integrals have widespread applications across various disciplines. In physics, they are used to calculate work done by a variable force, displacement, and other quantities involving accumulated change. In engineering, they find use in determining areas of irregular shapes, volumes of solids of revolution, and moments of inertia. Economists use definite integrals to calculate total cost, total revenue, and consumer surplus.
In this specific example, the integral represents the area under the curve y = (2/3)x^(2/3) from x = 1 to x = 64. This area has a practical interpretation depending on the context in which the function (2/3)x^(2/3) is defined. If it represents a rate of change (e.g., velocity), then the definite integral gives the total accumulated change (e.g., displacement) over the given interval.
Frequently Asked Questions (FAQ)
Q1: What if the exponent was negative?
A1: The power rule still applies, but you need to be careful. If the new exponent (n+1) becomes zero, you'll end up dividing by zero, which is undefined. The natural logarithm function handles integration when the exponent is -1.
Q2: Can I use numerical methods to solve this integral?
A2: Yes, numerical methods like the trapezoidal rule or Simpson's rule provide approximate solutions for definite integrals, especially when finding an analytical solution is difficult or impossible. However, for this specific problem, an analytical solution is straightforward.
Q3: What if the limits of integration were different?
A3: The process remains the same. Simply substitute the new upper and lower limits into the antiderivative and subtract the results.
Q4: Is there any other way to solve this integral?
A4: While the power rule offers the most straightforward approach for this particular integral, other techniques like substitution or integration by parts might be necessary for more complex integrals.
Conclusion
Evaluating the definite integral ∫₁⁶⁴ (2/3)x^(2/3) dx involves a straightforward application of the power rule of integration and the fundamental theorem of calculus. The step-by-step process detailed above demonstrates how to find the antiderivative, evaluate it at the limits of integration, and obtain the numerical value representing the signed area under the curve. Understanding this fundamental concept is crucial for grasping more advanced concepts in calculus and its applications in various fields. The solution, 409.2, provides a precise value for the area, allowing for a clear interpretation within the context of the problem. Remember to always check your work and understand the underlying principles, ensuring a strong foundation in integral calculus.
Latest Posts
Latest Posts
-
How To Get Tinder Gold With Chegg
Sep 22, 2025
-
Solve The Given Initial Value Problem Chegg
Sep 22, 2025
-
How To Cancel Renewell On Chegg
Sep 22, 2025
-
How To Delete A Question On Chegg
Sep 22, 2025
-
2 Naphthol Reacting With Naoh Formula
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Integral. 64 2 3 X X Dx 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.